例一：

-

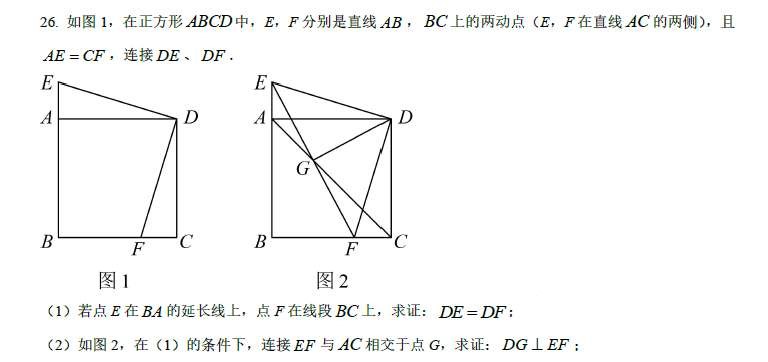
解：

设：∣∣bc∣∣=BC；∣∣ad∣∣=AD；∣∣ae∣∣=AE；∣∣fc∣∣=FC；∣∣ba∣∣=ABbc=(x,0)；ad=(x,0)；ae=(0,x2)；fc=(x2,0)；ba=(0,x)得:ba+bc=bd=(x,x)ea+ad=ed=(x,−x2)db+dc=dc=(0,−x)dc+cf=df=(−x2,−x)∣∣df∣∣=[df,df]；∣∣ed∣∣=[ed,ed]∣∣ed∣∣=∣∣df∣∣=ED=DFcosθ=[df,ed]∣∣ed∣∣∣∣df∣∣cosθ=0=90o⇔∠EDF显然:DG⊥EF\begin{align*} &\text{设：}\\ &||bc||=BC\text{；}||ad||=AD\text{；}||ae||=AE\text{；}||fc||=FC\text{；}||ba||=AB\\ &bc = (x,0)\text{；}ad=(x,0)\text{；}ae=(0,x_2)\text{；}fc=(x_2,0)\text{；}ba=(0,x)\\ &\text{得:}\\ &ba+bc=bd=(x,x)\\ &ea+ad=ed=(x,-x_2)\\ &db+dc=dc=(0,-x)\\ &dc+cf=df=(-x_2,-x)\\ &||df||=\sqrt{[df,df]}\text{；}||ed||=\sqrt{[ed,ed]}\\ &||ed||=||df||=ED=DF\\ &cos\theta=\frac{[df,ed]}{||ed||||df||}\\ &cos\theta=0=90^o\Leftrightarrow\angle EDF\\ &\text{显然:}DG\perp EF \end{align*}

例二：

-

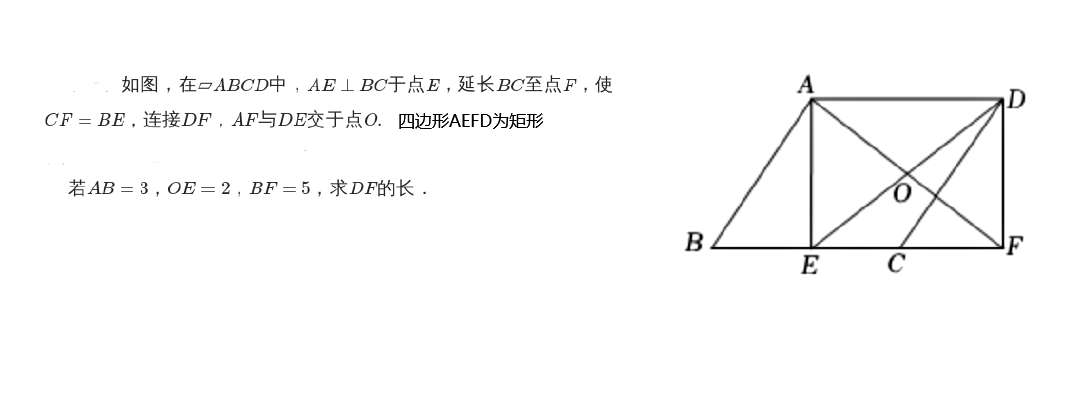
解：

设:∣∣bf∣∣=BF；∣∣be∣∣=BE；∣∣eo∣∣=EO；∣∣cf∣∣=CF；∣∣ba∣∣=BA；∣∣ef∣∣=EF显然且设:bf=(5,0)；be=(x,0)；cf=(x,0)；ba=(x,y)；ef=(5−x,0)得:ba+ed=ea=(0,y)ea+ef=ed=(5−x,y)eo=(5−x2,y2){∣∣ba∣∣=3∣∣eo∣∣=2解得{x=1.8y=2.4∴y=AE=DE=2.4\begin{align*} &\text{设:}\\ &||bf||=BF\text{；}||be||=BE\text{；}||eo||=EO\text{；}||cf||=CF\text{；}||ba||=BA\text{；}||ef||=EF\\ &\text{显然且设:}\\ &bf=(5,0)\text{；}be=(x,0)\text{；}cf=(x,0)\text{；}ba=(x,y)\text{；}ef=(5-x,0)\\ &\text{得:}\\ &ba+ed=ea=(0,y)\\ &ea+ef=ed=(5-x,y)\\ &eo=(\frac{5-x}{2},\frac{y}{2})\\ & \left\{ \begin{aligned} ||ba||=3 \\ ||eo||=2 \\ \end{aligned} \right. &\\ &\text{解得} \left\{ \begin{aligned} x&=1.8 \\ y&=2.4 \\ \end{aligned} \right. &\\ &\therefore y=AE=DE=2.4 \end{align*}

例三：

-

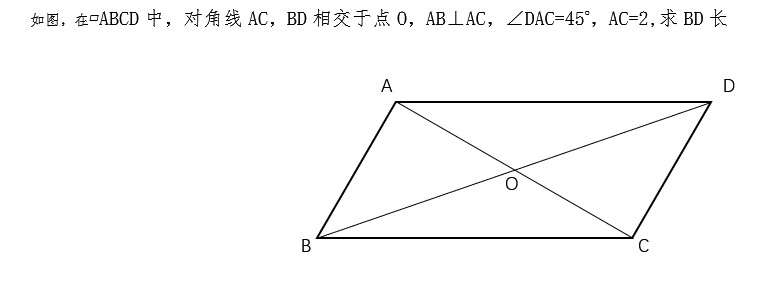
解：

设:∣∣ba∣∣=BA；∣∣bc∣∣=BC；∣∣bd∣∣=BD得:AD//BC⇔∠DAC=∠ACB=45o⇔BA=ACba=(2,y)；bc=(22,0)[ba,ba]=2y=2ba+bc=bd∣∣bd∣∣=25\begin{align*} &\text{设:}\\ &||ba||=BA\text{；}||bc||=BC\text{；}||bd||=BD\\ &\text{得:}\\ &AD//BC\Leftrightarrow\angle DAC=\angle ACB=45^o\Leftrightarrow BA=AC\\ &ba=(\sqrt{2},y)\text{；}bc=(2\sqrt{2},0)\\ &\begin{aligned} \sqrt{[ba,ba]}&=2\\ y&=\sqrt{2} \end{aligned}\\ &ba+bc=bd\\ &||bd||=2\sqrt{5}\\ \end{align*}

例四：

-

解：

显然:PC=(x−2)2+(x33)2PB=x2+(x33)22f(x)=(x−2)2+(x33)2+x2+(x33)22dfdx=(2 x−3) 4 x2−12 x+12 ∣x∣+2 x3−6 x2+6 x(2 3 x2−2⋅3 3 x+2⋅3 3) ∣x∣令dfdx=0解得x=0则f(0)=2∴min(PC+PB2)=2\begin{align*} \begin{aligned} &\text{显然:}\\ &PC=\sqrt{(x-2)^2+(x\frac{3}{3})^2}\\ &PB=\frac{\sqrt{x^2+(x\frac{\sqrt{3}}{3})^2}}{2}\\ &f(x)=\sqrt{(x-2)^2+(x\frac{3}{3})^2}+\frac{\sqrt{x^2+(x\frac{\sqrt{3}}{3})^2}}{2}\\ &\frac{df}{dx}=\dfrac{\left(2\,x-3\right)\,\sqrt{4\,{x}^{2}-12\,x+12}\,\left|x\right|+2\,{x}^{3}-6\,{x}^{2}+6\,x}{\left(2\,\sqrt{3}\,{x}^{2}-2\cdot 3\,\sqrt{3}\,x+2\cdot 3\,\sqrt{3}\right)\,\left|x\right|}\\ &\text{令}\frac{df}{dx}=0\\ &\text{解得}x=0\\ &\text{则}f(0)=2\\ &\therefore min(PC+\frac{PB}{2})=2 \end{aligned} \end{align*}

虽然，例四其实连算的不用算……